Математичні властивості

Золотий перетин можна обчислити безпосередньо з означення:

Дане рівняння дає . Підставляючи цю рівність у ліву частину:

Скоротивши отримаємо:

Помноживши обидві частини на після перестановки отримаємо:

φ2 − φ − 1 = 0.

Це квадратне рівняння має два розв'язки, один з яких є додатнім

- ірраціональне число алгебри, рішення квадратного рівняння:

x2 − x − 1 = 0, звідки, виходять співвідношення:

φ2 = φ + 1

- представляється через тригонометричні функції:

- представляється у вигляді нескінченного ланцюжка квадратного коріння:

- представляється у вигляді нескінченного ланцюгового дробу

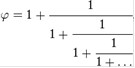
відповідними дробами якої служать відносини послідовних чисел Фібоначчі . Таким чином

При цьому члени послідовності збігаються до поперемінно - один елемент знизу, наступний згори і т.д. Наприклад

Формула Біне виражає за допомогою значення числа Фібоначчі в явному вигляді:

Окрім цього, послідовні степені числа задовільняють рекурентному співвідношенню ідентичному до чисел Фібоначчі:

Спіраль Фібоначчі (Рисунок 2) є наближенням золотої спіралі.

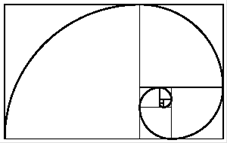
Рисунок 2 - Спіраль Фібоначчі

є знаменником геометричної прогресії, кожен член якої, починаючи з третього, рівний сумі двох попередніх.

Золотий перетин виступає у правильній пентаграмі (Рисунок 3), який вважався магічним символом у багатьох культурах. Точка перетину сторін ділить їх у золотій пропорції. Більша частина сторони також ділиться у золотій пропорції іншою точкою перетину.Пентаграм містить п'ять гострокутних та п'ять тупокутних золотих трикутників. У кожному з них співвідношення довжини довшої та коротшої сторони утворює золотий перетин.

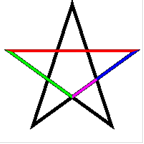
Рисунок 3 - Золотий перетин у правильній пентаграмі

Геометрична побудова. Золотий перетин відрізка AB можна побудувати таким чином: у точці B відновлюють перпендикуляр до AB, відкладають на ньому відрізок BC, рівний половині AB, на відрізку AC відкладають відрізок CD, рівний BC, і нарешті, на відрізку AB відкладають відрізок AE, рівний AD (рисунок 3). Тоді

Подібні статті

Іммобілізація ферментів та клітин мікроорганізмів
Методи іммобілізації універсальні для всіх типів біокаталізаторів - індивідуальних ферментів, клітин, субклітинних структур, комбінованих препаратів. Поряд з іммобілізацією ферментів останнім часом все більшу увагу приділяють іммобіліз ...

Біологія Х-вірусу картоплі
Віруси не можуть самостійно поширюватись у природі. Допомагають їм у цьому насамперед комахи-переносники (віроформні комахи). Фітопатогенні віруси найчастіше переносять попелиці, трипси, цикади, кліщі й деякі листогризучі комахи. Наприклад ...